RELACIONES Y GRAFICAS
RELACION DIRECTA
Se dice que una variable (por ejemplo y) es directamente proporcional a otra variable (por ejemplo x), cuando al variar la una en alguna proporción, la otra varía en la misma proporción.
Simbólicamente se escribe:
Toda proporcionalidad se puede convertir en una igualdad colocando una constante, llamada contante de proporcionalidad.
Gráfica de una relación directa
La gráfica de una relación directa siempre dará una recta que pase por el origen, es decir:
Nota: Toda relación directa es una relación lineal, pero no toda relación lineal es una relación directa.
Ejercicios de relación directa
Dadas las siguientes
relaciones, en forma de tabla de valores, indique cuales SI y cuales NO son
relaciones directas, Justificando su respuesta:
En la tabla A observamos que de 0,05 a 0,15, la X se triplica, y de 10 a 30, la F también se triplica, por lo tanto es una relación directa porque varían en la misma proporción.👍SI
En la tabla B observamos que de 0,8 a 0,4, la a se hizo la mitad, y de 40 a 20, la T también se hizo la mitad, por lo tanto es una relación directa porque varían en la misma proporción.👍SI
En la tabla C observamos que de 2 a 4, la P se duplica, y de 25 a 75, la L se triplica, por lo tanto NO es una relación directa porque NO varían en la misma proporción.👎NO
RELACION LINEAL
y = mx + b
Dos variables (por ejemplo y y x) se dice que están en relación lineal cuando cumplen la forma: y = mx + b, donde m representa la pendiente y b el corte con el eje de las ordenadas.
Pendiente.- Se define pendiente a la tangente del ángulo de inclinación (ángulo formado entre una horizontal y la recta dada).
Es importante tener en cuenta que el ángulo de inclinación debe girar en sentido antihorario.
La recta será creciente cuando el ángulo de inclinación sea agudo (lo cual nos dará una pendiente positiva); pero será decreciente cuando el ángulo de inclinación sea obtuso (lo cual nos dará una pendiente negativa).
Línea Vertical.- Es la línea imaginaria que se forma al unir las posiciones de una masa puntual que cae libremente partiendo del reposo.
Línea Horizontal.- Es toda línea perpendicular a la vertical.
Ecuaciones de la relación lineal
Forma Particular: y = mx + b
Forma General: Ax + By + C = 0
Forma Simétrica: x/a + y/b = 1
Gráfica de una relación lineal
La gráfica de una relación lineal siempre será una línea
recta que puede cruzar en cualquier punto del eje de las ordenadas.
RELACION CUADRATICA
Se dice que una variable (por ejemplo y) es relación cuadrática con otra variable (por ejemplo x), cuando al variar la una en alguna proporción, la otra varía en el cuadrado de dicha proporción.
Matemáticamente se escribe:
Se lee: y es directamente proporcional al cuadrado de x
Esto significa que si x se duplica la y se cuadruplica, o si x se triplica, la y se hace 9 veces más, o si la x se hace la cuarta parte, la y se hace la dieciseisava parte.
Gráfica de una relación cuadrática
La gráfica de una relación cuadrática será una parábola:
Por ejemplo, entre el área y el radio del círculo existe una relación
cuadrática:
Donde π sería la constante de proporcionalidad
Ejercicios de relación cuadrática
Demostrar algebraicamente que si y es directamente proporcional al cuadrado de x, al triplicarse la x, la y se hace 9 veces más.
RELACION CUBICA
Se dice que y es directamente proporcional al cubo de x cuando al variar la x en alguna proporción, la y varía en el cubo de dicha proporción; es decir si x se duplica, la y se hará 8 veces más, o si la x se hace la tercera parte, la y se hará la veintisieteava parte.
Matemáticamente se escribe:
Se lee: y es directamente proporcional al cubo de x
Gráfica de una relación cúbica
La gráfica de una relación cúbica será una parábola cúbica:
Por ejemplo, entre el volumen y el radio de una esfera existe una relación cúbica:
Donde (4/3)π sería la constante de proporcionalidad
Ejercicios de relación cúbica
Demostrar algebraicamente que si y es directamente proporcional al cubo de x, si x se triplica, la y se hará 27 veces más.
RELACION INVERSA
Se dice que y es inversamente proporcional a x, cuando al variar la x en alguna proporción, la y varía en el inverso de dicha proporción. Es decir si x se duplica, y se hace la mitad; y si x se hace la tercera parte, la y se hará el triple.
Matemáticamente se representa:
Se lee y es inversamente proporcional a x
Gráfica de una relación inversa
La gráfica de una relación cúbica será una hipérbola:
Por ejemplo, entre la rapidez y distancia hay una relación directa, pero entre rapidez y tiempo existe una relación inversa:
v = d/t
Ejercicios de relación inversa
Demostrar algebraicamente que si y es inversamente proporcional a x, al triplicarse la x, la y se hará la tercera parte.
RELACION
INVERSA CUADRATICA
Se dice que y es
inversamente proporcional al cuadrado de x, cuando al variar la x en
alguna proporción, la y varía en el inverso del cuadrado de
dicha proporción. Es decir si x se duplica, y se
hace la cuarta parte; y si x se hace la tercera parte,
la y se hará 9 veces más.
Matemáticamente se representa:
Se lee y es inversamente proporcional al
cuadrado de x
Ejercicios de relación inversa cuadrática
Demostrar
algebraicamente que si y es inversamente proporcional al
cuadrado de x, al triplicarse la x, la y se
hará la novena parte.
RELACION
INVERSA CUBICA
Similar a las
anteriores relaciones inversas.
Gráfica de una relación inversa cuadrática o cúbica
La gráfica de cualquier relación inversa, sea cuadrática o cúbica será una hipérbola.
DESCARGATE! el folleto completo de Relaciones y Gráficas y encuentra más de 60 EJERCICIOS Y PROBLEMAS para que puedas practicar.













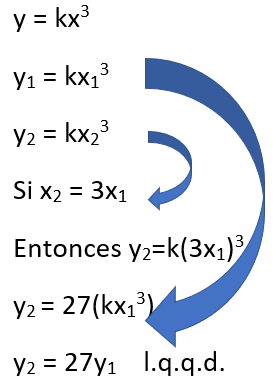










0 Comentarios