LA LINEA RECTA

Una línea recta es una sucesión infinita de puntos que siguen la misma dirección

Ecuaciones de la línea recta:

Existen tres formas de representar a una línea recta: la forma PARTICULAR, la forma GENERAL y la forma SIMETRICA.

FORMA PARTICULAR DE LA RECTA:

y = mx +b siendo m la pendiente y b la ordenada en el origen.

La pendiente (m) se define como la TANGENTE del ángulo de inclinación. (El ángulo de inclinación es aquel que se forma con cualquier horizontal y la línea recta, GIRANDO EN SENTIDO ANTIHORARIO).

Si este ángulo es agudo, la pendiente será positiva; pero si es obtuso, la pendiente será negativa.

Fórmula para encontrar la pendiente:

m = tan θ

m = (y2 – y1)/(x2 – x1)

m = Δy/Δx

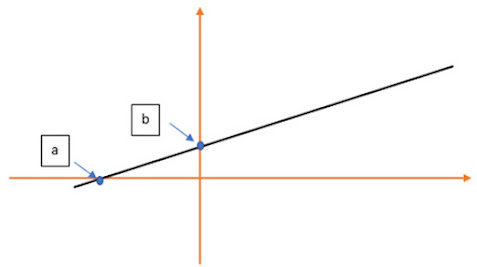
La ordenada (b) en el origen es el punto donde corta la recta con el eje de las ordenadas.

EXPLICACIÓN:

FORMA GENERAL DE LA RECTA:

Para encontrar la forma general basta con igualar todos los valores a 0, siendo expresiones algebraicas enteras todos los términos de la ecuación.

Ax +By +C = 0

Si despejamos la letra y de la ecuación tenemos:

By = -Ax - C

y = (-A/B)x - C/B
y = mx + b
Entonces la pendiente sería: m = -A/B ; y la ordenada en el origen b = -C/B

FORMA SIMÉTRICA DE LA RECTA:

Para encontrar la forma simétrica debemos igualar todos los valores a 1, teniendo únicamente las x, y en los numeradores de cada fracción:

x/a + y/b = 1

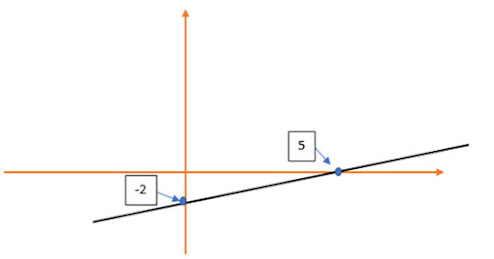
a es el punto de corte con X y b es el punto de corte con Y.

EJERCICIO:

1. Dada las siguiente ecuación representa la recta en la forma general, particular, simétrica y grafica.

2X - 5Y =10

Forma general: 2x -5y -10 = 0

Forma particular: (despejamos Y):

- 5y = -2x + 10

5y = 2x -10 (cambiamos de signo tanto a Y para que sea positiva y hacemos lo mismo con la X y el 10 para no alterar la ecuación).

y = (2/5)x – 10/5 (separamos letras y números para dejar a Y sola, el 5 pasa de multiplicar a dividir en el otro lado)

Obtenemos el resultado: y = (2/5)x -2

Forma Simétrica:

2x -5y = 10 Separamos letras y números

Para igualar todo a uno debemos dividir al 10 para 10, así obtendremos que la ecuación es igual a uno, pero para no alterar los valores debemos dividir al 2x y 5y para 10 también, así obtenemos lo siguiente:

2x/10 -5y/10 = 10/10

x/5 – y/2 = 1 (simplificamos los valores)

x/5 + y/-2 = 1 (dejamos X y Y expresados de forma positiva, en este caso convertimos a Y en positiva cambiando de signo al denominador de la fracción -2 y así obtenemos la forma simétrica).

GRAFICO:

Para poder graficar la línea recta podemos usar los valores dados por la forma PARTICUAR, en este caso Y = (2/5)x -2. La pendiente que vamos a graficar se representa con 2/5 porque es el coeficiente de la x, siendo 2 la variación en Y y 5 la variación en X, esto quiere decir que los puntos de la recta van a variar en 2 puntos en Y y en 5 puntos en X desde el punto de corte con Y que en este caso sería -2. El punto de corte con Y que se lo representa con b nos indica en qué punto empezar a dibujar:

MIRA LA RESOLUCION

FÓRMULAS PARA ENCONTRAR LA ECUACIÓN DE LA LÍNEA RECTA

A PARTIR DE UN PUNTO Y LA PENDIENTE:

(y– y₁) = m (x – x₁)

DADOS DOS PUNTOS:

(y – y₁) / (x – x₁) = (y₂ – y₁) / (x₂ – x₁)

VIDEO EXPLICATIVO

PROBLEMAS

1) Encuentre la ecuación de la recta que pasa por el punto A(-5,2) y tiene una pendiente igual a -3. Grafique su recta.

2) Encuentre la pendiente de la recta que pasa por los dos puntos A(-3,-5) y B(4,3). Determine su ecuación y grafique su recta.

Condiciones de paralelismo y perpendicularidad

Paralelismo

Si dos rectas son paralelas, entonces sus pendientes son iguales.

m1 = m2

Perpendicularidad

Si dos rectas son perpendiculares, sus pendiente son inversas y opuestas, es decir que el producto de dichas pendientes será -1.

m1 = -1/m2

m1.m2 = -1

MIRA EL SIGUIENTE VIDEO DONDE EXPLICO CÓMO PUEDES ENCONTRAR Y GRAFICAR DE FORMA FÁCIL RECTAS PARALELAS Y PERPENDICULARES:

PROBLEMAS

3) Una recta L1 pasa por el punto A(-1,4) y es paralela a la recta L2 que pasa por los puntos B(0,3) y C(6,-2). Hallar la ecuación de la recta L1 y grafique las dos rectas.

4) Una recta L1 pasa por el punto A(7,4) y es perpendicular a la recta L2 que pasa por los puntos B(-2,6) y C(0,1); encuentre la ecuación de la recta L1 y grafique las dos rectas.

MATECH77

Header Ads Widget