SISTEMAS DE ECUACIONES
Un sistema
de ecuaciones está formado por dos o más ecuaciones con dos o más variables,
cuyos valores deben satisfacer la igualdad de todas las ecuaciones del sistema.
Por lo
general, para resolver un sistema de ecuaciones se necesita tener el mismo
número de ecuaciones que de incógnitas. Es decir, si tenemos un sistema con dos
incógnitas, necesitaremos tener dos ecuaciones, si tenemos con tres incógnitas,
necesitaremos tres ecuaciones, y así por el estilo.
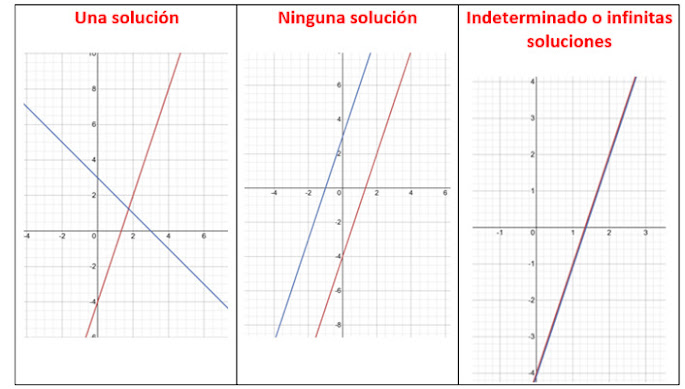
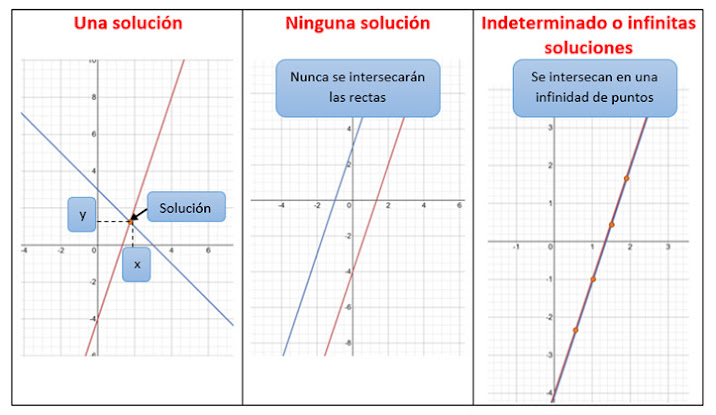
En un
sistema de ecuaciones de primer grado con dos incógnitas se pueden presentar
las siguientes situaciones.
A continuación estudiaremos los siguientes métodos para resolver un
sistema de ecuaciones:
Método de adición y sustracción o reducción
Se debe eliminar una de las incógnitas de tal forma que llegamos a obtener
una ecuación con una incógnita que resolvemos despejando la variable. Para eliminar
una de las incógnitas, sus coeficientes deben ser opuestos, en caso de que no
lo sean debemos encontrar el mínimo común múltiplo (mcm) de dichos coeficientes,
y multiplicar a toda la ecuación por el número que resulta de dividir el mcm
para el coeficiente, teniendo cuidado de que los signos sean opuestos con la
finalidad de eliminar la incógnita al momento de sumar. Para encontrar la otra incógnita
sustituimos el valor de la encontrada en cualquier ecuación y despejamos.
Ejemplo
1.- 3x – 2y = 7
5x +
3y = 37
Reproduce el vídeo para ver la resolución:
Método de sustitución
Se debe despejar una de las incógnitas de cualquier ecuación, y sustituir
en la otra ecuación, de tal forma que llegamos a obtener una ecuación con una variable
que resolvemos despejando la variable. Para encontrar la otra incógnita sustituimos
el valor de la encontrada en cualquier ecuación y despejamos.
Ejemplo
1.- 2x + y = 7
3x - 2y
= 14
Reproduce el vídeo para ver la resolución:
Método de los determinantes
Debemos formar determinantes con los coeficientes de las incógnitas y el
término independiente, de la forma que se indica debajo, y después resolvemos
el determinante.
Dado el sistema:
a1x + b1y = c1
Se forman los siguientes determinantes que deben ser resueltos
Ejemplo
1.- x – 2y = 9
3x -4y
= 15
3x + 4y - 3z = 2
2x + 3y - 2z = 2
Reproduce el vídeo para ver la resolución:
Método gráfico
Debemos graficar cada ecuación utilizando una tabla de valores, o de
forma directa con los valores de la pendiente y ordenada en el origen. La solución
es el punto donde se intersecan ambas rectas. Recordamos que se podían dar las
siguientes condiciones:
Ejemplo
1.- 2x + y = 6
3x – y = 4







0 Comentarios